Research Snippets

Applied Algebraic Topology

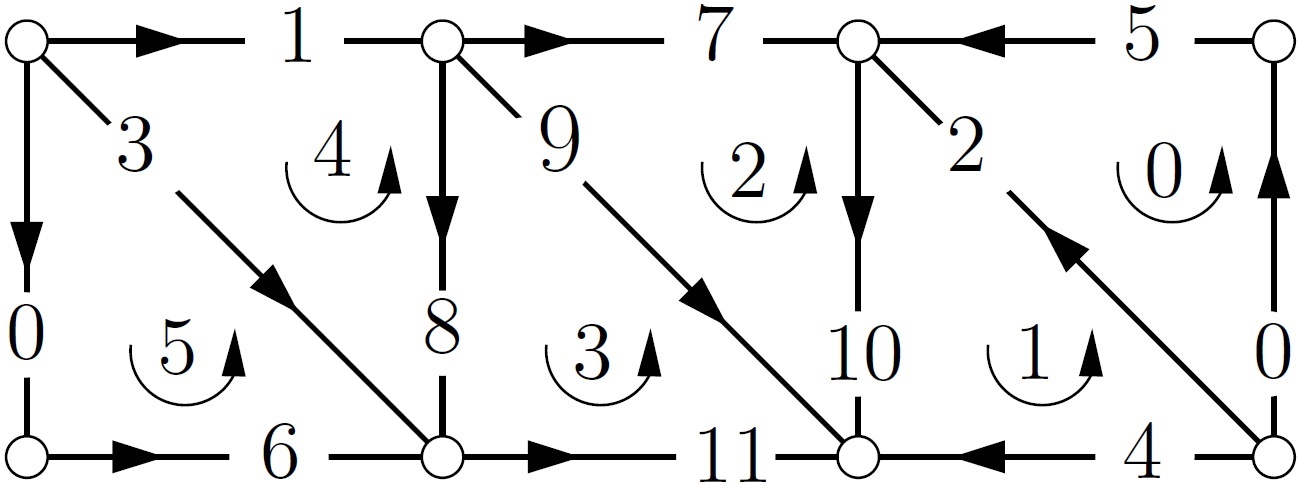
Optimal homologous cycles, total unimodularity, and linear programming (SIAM J. Computing, 2011, 40(4), 26–40. Talk.

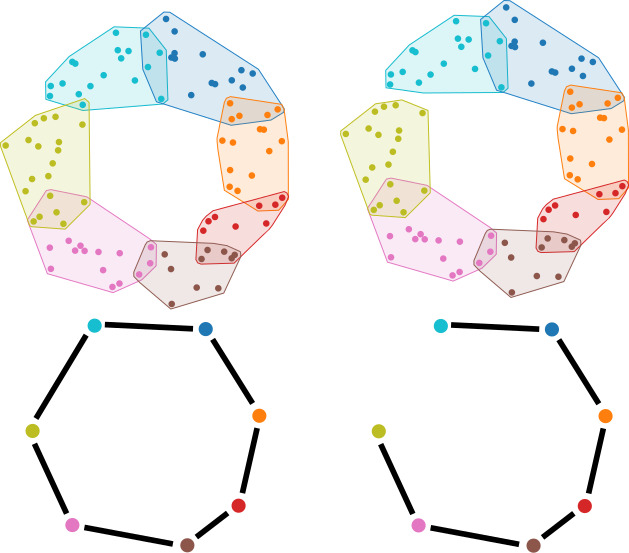
Synopsis: We show the equivalence of matrix total unimodularity and the property of the relative homology groups of a simplicial complex being torsion-free (referred to as relative-torsion free, RTF). A 2-complex is RTF if it has no Möbius subcomplexes. When the simplicial complex is RTF, several otherwise hard problems on the homology groups could be solved in polynomial time using linear programming.

Steinhaus Filtration and Stable Paths in the Mapper (SoCG 2025). Talk video.

Synopsis: We define a new filtration called the Steinhaus filtration built from a single cover based on a generalization of Jaccard distance. We then develop a language and theory for stable paths within the Steinhaus filtration. This framework can be applied to several applications where a metric may not be defined but a cover is readily available.

Geometric Measure Theory

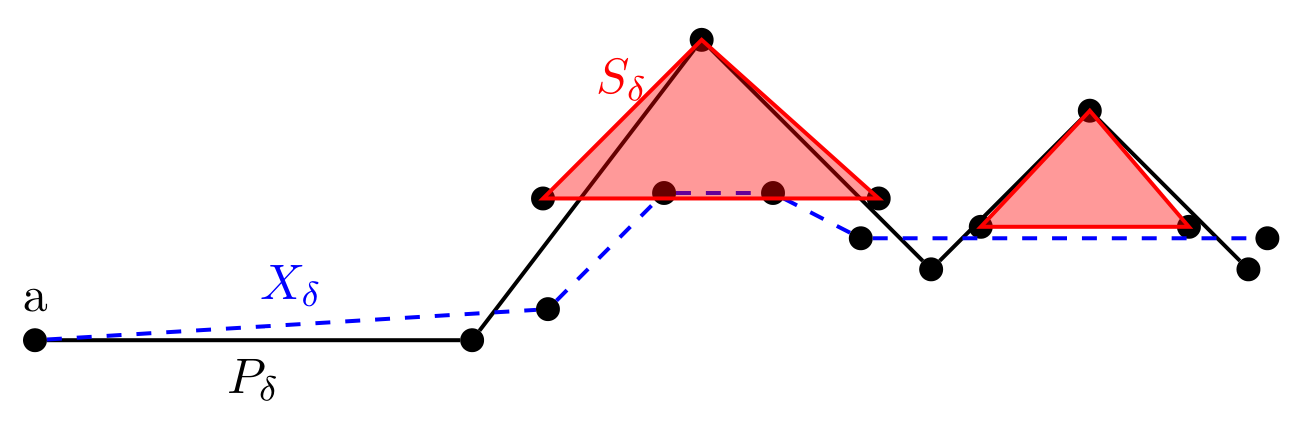
Flat norm decomposition of integral currents (Journal of Computational Geometry, 7, 1, 2016, 285–307). Talk.

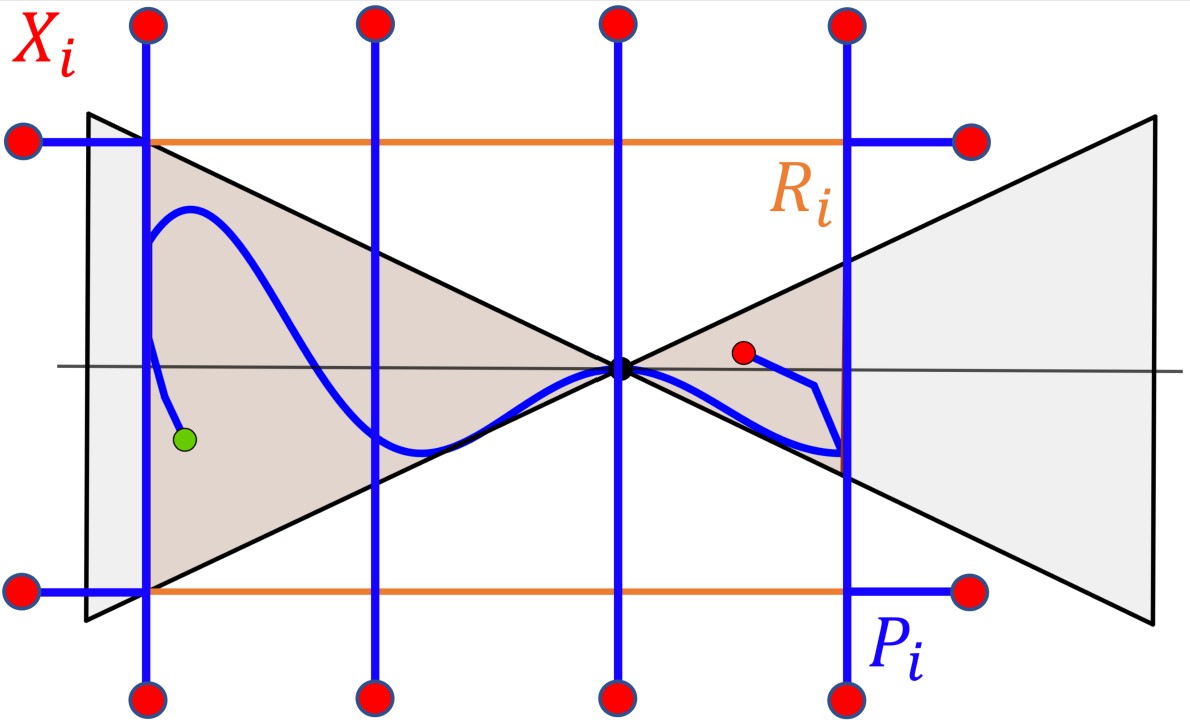
Synopsis: When is the flat norm decomposition of an integral current also integral? This turns out to be quite a tricky question, as indicated by the related observation that filling a curve with an oriented surface could sometimes be "cheaper by the dozen"! On the other hand, integrality in the simplicial setting is guaranteed for many relevant cases. Here we develop an analysis framework to push the result from the simplicial setting to the continuous setting.

The Maximum Distance Problem and Minimal Spanning Trees (Intl. J. Analysis and Applications, 2021, 19, 5, 633–659). Talk.

Synopsis: We study a fat generalization of the classical TSP where we seek a shortest 1D curve (or a 1D set, more generally) which when fattened by a radius \(s\) covers a given 2D set. Given a compact \(E \subset \mathbb{R}^n\) and \(s>0\), the maximum distance problem (MDP) seeks a compact and connected subset of \(\mathbb{R}^n\) of smallest one dimensional Hausdorff measure whose \(s\)-neighborhood covers \(E\). For \(E \subset \mathbb{R}^2\), we prove that minimizing over minimum spanning trees that connect the centers of balls of radius \(s\), which cover \(E\), solves the MDP.

Mathematical Aspects of 3D Printing

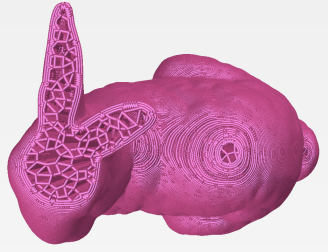
Continuous Toolpath Planning in a Graphical Framework for Sparse Infill Additive Manufacturing (Computer-Aided Design, 127, Oct 2020, 102880). Talk.

Synopsis: We develop a new method to generate continuous toolpaths with no crossovers in sparse infill 3D printing. We define and use an Euler Transformation of general polyhedral complexes, which guarantees that every vertex has an even degree in the graph of the complex. Hence an Eulerian tour that covers every edge exactly once is guaranteed to exist. Our framework handles most domains with complex geometry/topology in layer-by-layer printing. We validate our method on simple and complex print domains.

SFCDecomp: Multicriteria optimized tool path planning using space-filling curves (IJCGA, 31, 04, 2021, 193–220). Talk.

Synopsis: We explore efficient optimization of toolpaths based on multiple criteria for large instances of dense infill 3D printing prolems. We develop SFCDecomp, a space filling curve based decomposition framework to solve large instances of 3D printing problems efficiently by solving these optimization subproblems independently. Strength testing of a tensile test specimen printed with tool paths that maximize or minimize adjacent layer edge overlaps reveal significant differences in tensile strength between the two classes of prints.

Lattice Problems and Integer Optimization

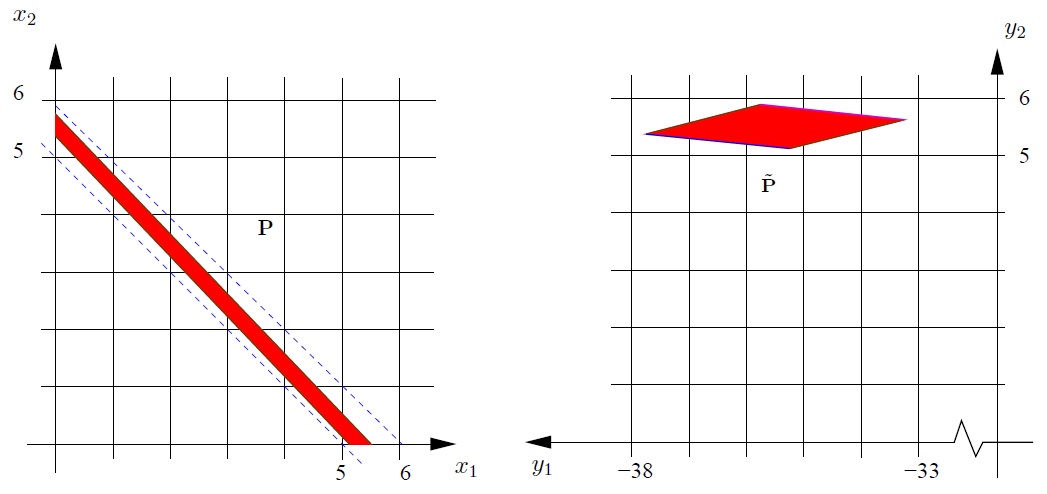
Column basis reduction, and decomposable knapsack problems (Discrete Optimization, 2009, 6(3), 242–270). Instances. Overview talk.

Synopsis: We propose a very simple preconditioning method called rangespace reformulation for integer programming feasibility problems: replacing the problem \(\{ \mathbf{b}' \leq A \mathbf{x} \leq \mathbf{b}, \mathbf{x} \in \mathbb{Z}^n \}\,\) with \(\,\{\mathbf{b}' \leq AU \mathbf{y} \leq \mathbf{b}, \mathbf{y} \in \mathbb{Z}^n\}\), where \(U\) is a unimodular matrix computed via basis reduction, to make the columns of \(AU\) short and nearly orthogonal. We also study a family of IP instances called decomposable knapsack problems (DKPs), which are knapsack problems with a constraint vector of the form \(\mathbf{p}M + \mathbf{r}\) with \(M \gg 0\). We prove (i) hardness results for branch-and-bound branching on individual variables of the DKPs; (ii) that they are easy, if one branches on the constraint \(\mathbf{p}^T\mathbf{x}\) instead; and (iii) that branching on the last few variables in the rangespace reformulation is equivalent to branching on \(\mathbf{p}^T\mathbf{x}\).

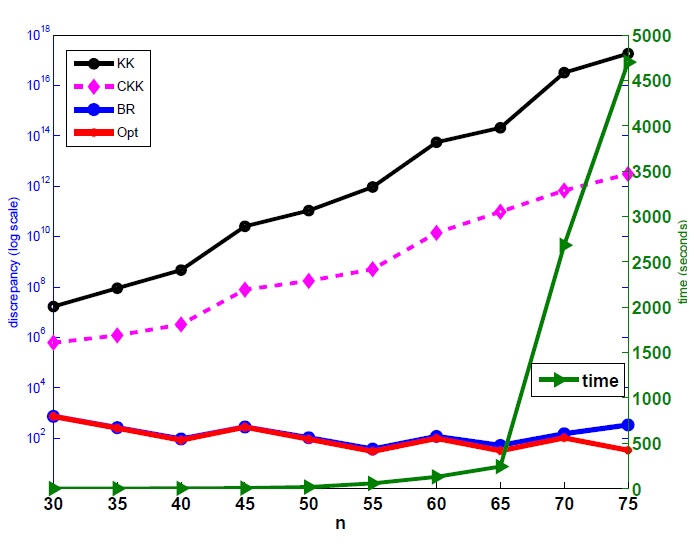
Lattice-based Algorithms for Number Partitioning in the Hard Phase (Discrete Optimization, 2012, 9(3), 159–171). Talk.

Synopsis: The number partitioning problem (NPP) is to divide \(\{a_1,...,a_n\}\) into two disjoint subsets such that the difference between the two subset sums - the discrepancy, \(\Delta\), is minimized. With \(a_j\)s chosen uniformly from \([1,R]\), \(R > 2^n\) gives the hard phase, when there are no equal partitions with high probability. We reduce NPP in the hard phase to the closest vector problem (CVP). We can solve the original problems by making polynomial numbers of calls to a CVP oracle. In practice, we implement a heuristic which applies basis reduction (BR) to several CVP instances. We also propose a truncated NPP algorithm, which finds approximate minimum discrepancies for instances on which the BR approach is not effective.

Computational Biology

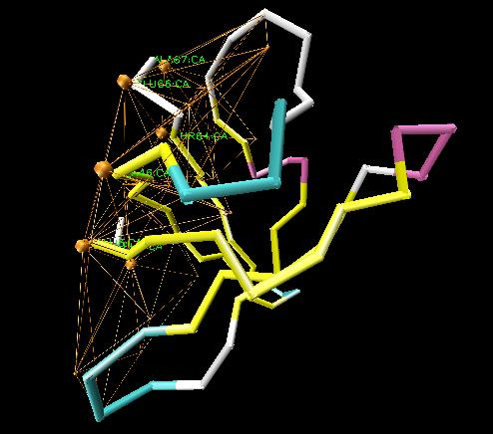
Four-body scoring function for mutagenesis (Bioinformatics, 2007, 23(22), 3009–3015). Overview talk.

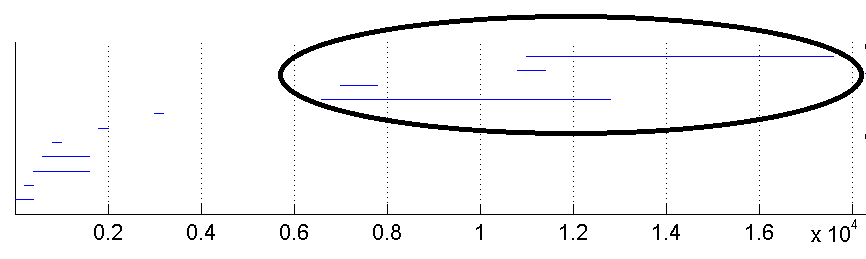
Synopsis: We develop a Delaunay tessellation-based four-body scoring function to predict the effects of single and multiple residue mutations on the stability and reactivity of proteins. We also develop an efficient method for screening huge numbers of mutants of a protein, called combinatorial mutagenesis. In one study, 64 million mutants of the protein 1CSQ, with six of its residues being changed to all possible (20) amino acids, were screened within a few hours on a PC, and all five stabilizing mutants reported were correctly identified as stabilizing by combinatorial mutagenesis.

Topological features in cancer gene expression data (in PSB 2015, 20, 108–119). Talk.

Synopsis: We develop a new method using topological persistence to analyze cancer gene expression datasets. We circumvent the problem of high dimensionality by dualizing the data, i.e., by studying genes as points in the sample space. We identify a small relevant subset from tens of thousands of genes while simultaneously identifying nontrivial higher order topological features, i.e., holes, in the data.

Biomedical Applications

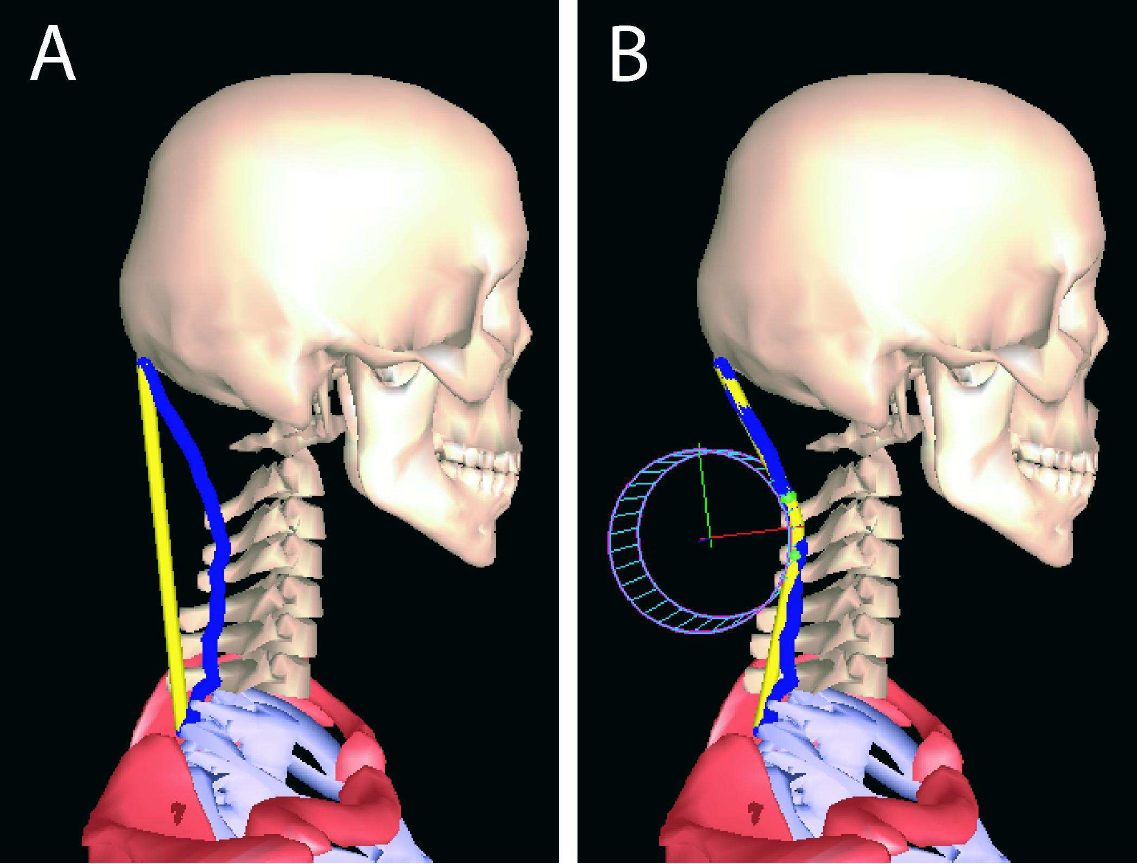
Neck muscle paths and moment arms are significantly affected by wrapping surface parameters (Comp. Met. Biomech. Biomed. Engg, 2012, 15(7), 735–744).

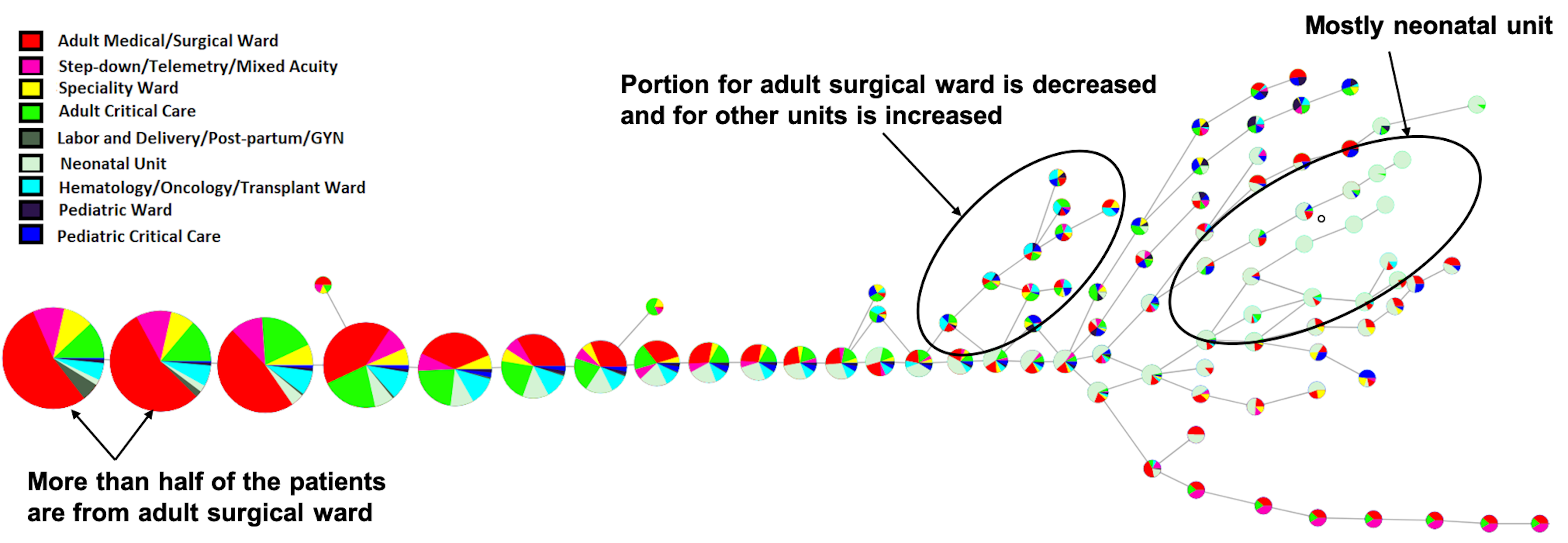
Synopsis: We studied the effects of wrapping surfaces on muscle paths and moment arms of the neck muscle, semispinalis capitis. Sensitivities to wrapping surface size and the kinematic linkage to vertebral segments were evaluated. Kinematic linkage, but not radius, significantly affected the accuracy of model muscle paths compared to centroid paths from images. Both radius and linkage affected the moment arm significantly. This study highlights the sensitivity of moment arms to wrapping surface parameters and the importance of including multiple postures when evaluating muscle paths and moment arm.

A visual analytics framework for analysis of patient trajectories (In ACM BCB, 2019).

Synopsis: A new visual analytics approach to analyze hospital patient trajectories in a scalable manner. We view the problem as one of structure discovery and tracking how structure evolves with time over the course of patients' stay at the hospital(s). Our approach helps to delineate subpopulations (i.e., subgroups of patients) that show divergent behavior. Initial results on a large data set from the Duke Antimicrobial Stewardship Outreach Network (DASON) database.

Publications
CV
Patent(s): US12118604B2

Events (Conferences, Workshops, etc.)

CG Week 2025, Kanazawa, Jun 23–27, 2025.
CG Week 2024, Athens, Jun 10–14, 2024.
Cascade RAIN Math Meeting, Portland, Apr 27, 2024.
Jon-Shmuel Halfway to Twelfty, Paris, Jul 4–7, 2023.
CG Week 2023, UT Dallas, Jun 12–16, 2023.
SIAM Conference on Mathematics of Data Science (MDS22), San Diego, Sep 26–30, 2022.
SIAM Conference on Discrete Mathematics (DM22), CMU, Jun 14–16, 2022.
SIAM PNW 21, WSU Vancouver, May 20–22, 2022.
JMM 2022, Online, Apr 6–9, 2022.
IMSI Workshop on The Mathematics of Soft Matter, Online, Feb 28–Mar 4, 2022.
Computational Persistence Workshop, Online, Nov 1–5, 2021.
JMM 2021, Online, Jan 2021.
SPM 2020, Online, June 2020.
WCOM Fall 2019, UBC, Vancouver, Sep 28, 2019.
CG Week 2019, Portland, OR, June 2019.
Optimization Methods in Vision and Image Processing, ICERM, Apr 29–May 3, 2019.
CGWeek and SoCG, Budapest, Hungary, June 2018.
Joint Mathematics Meetings, 2018, San Diego, CA.
SIAM PNW Biennial Meeting, Corvallis, OR, Oct 27-29, 2017.
SIAM Conference on Applied Algebraic Geometry, Atlanta, Jul 31-Aug 4, 2017.
AMS Spring Western Sectional Meeting (Special sessions: 1, 2, 3), Pullman, Apr 22-23, 2017.
Workshop on Topological Data Analysis in Biomedicine in ACM-BCB 2016.
Joint Mathematics Meetings (Special sessions 1 and 2), Seattle, Jan 6-9, 2016.
Workshop on Abstract Algebra and Algebraic Topology in Biomedicine in PSB 2016, Hawaii, Jan 4, 2016.
Mathematics in Data Science, ICERM, Jul 28-30, 2015.
International Symposium on Mathematical programming (ISMP), July 12-17, 2015.
Topology and Geometry of Networks and Discrete Metric Spaces, IMA, Apr 28-May 2, 2014.
Topological Systems: Communication, Sensing, and Actuation, IMA, Mar 3-7, 2014.
Topological Structures in Computational Biology, IMA, Dec 9-13, 2013.
Modern Applications of Homology and Cohomology, IMA, Oct 28-Nov 1, 2013.
Topological Data Analysis, IMA, Oct 7-11, 2013.
Modern Trends in Optimization Reunion II, IPAM, June 2013.
ASCR/BES Data Workshop, Bethesda, MD, Oct 24-25, 2011.
Applied Mathematics and Image Processing Summer Workshop at UTPA, May 31-Jun 1, 2011.
Modern Trends in Optimization and Its Application at IPAM, Sep 13-Dec 17, 2010.
STOC 2010
IMA short course on Applied Algebraic Topology, June 15-26, 2009.
AMS Spring Western Section Meeting 09